개요 및 정의

오늘은 자료구조 중 하나인 트리에 대해 다루어 보려합니다.
트리는 그래프의 일종으로 큐, 스택, 리스트 같은 선형 구조와는 달리 비선형 구조로 되어있으며 계층적 특징을 가지고있습니다.
또한 트리는 순환 구조를 가지지 않습니다.
여기서 순환 구조란, 노드의 연결 방향이 서로 순환하는 구조를 말합니다.
위 사진에서 만약에, H 노드와 I 노드가 서로 연결되어있다면 D노드, H노드, I노드는 순환구조입니다.
트리구조의 기본 용어
- 루트(Root) : 트리에서 가장 꼭대기에 위치한 노드
- 간선(Edge) : 노드와 노드를 잇는 연결선
- 단말 노드(Leaf) : 아래로 또 다른 노드가 연결되어 있지 않은 노드
- 내부 노드 : 단말 노드를 제외한 모든 노드
- 부모 노드 : 세 노드가 트리구조일 때 상단에 위치한 노드
- 자식 노드 : 세 노드가 트리구조일 때 부모노드와 연결된 하위의 노드
- 형제 노드 : 같은 부모 노드와 연결된 하위의 노드들
- 레벨(Level) : 특정 깊이를 가지는 노드의 집합. 루트 노드를 0으로 하여 아래로 내려갈수록 1씩 증가
- 깊이 : 루트노드에서 어떤 노드까지의 간선의 수
- 높이 : 루트노드에서 단말노드까지 가장 긴 간선의 수
- 서브 트리(Sub Tree) : 큰 트리에 속하는 작은 트리
트리의 종류 : 이진 트리(Binary Tree)
트리는 그 특징만 잘 지킨다면 어떤 것이든 트리가 될 수 있습니다. 따라서 그 종류도 많습니다.
이번에는 트리 중에서도 이진 트리에 대해 알아보겠습니다.
이진 트리 다음과 같은 특징을 갖는 트리를 말합니다.
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
- 나뉘어진 두 서브 트리도 모두 이진 트리이다.
- 노드는 반드시 왼쪽부터 채워져야한다.
쉽게 생각하면 모든 부모노드가 자식을 둘만 가지며 모든 서브트리의 부모노드 또한 자식을 최대 둘만 갖습니다.
이진 트리 또한 그 형태에 따라 포화 이진 트리(Full Binary Tree)와 완전 이진 트리(Complete Binary Tree)로 나뉩니다.
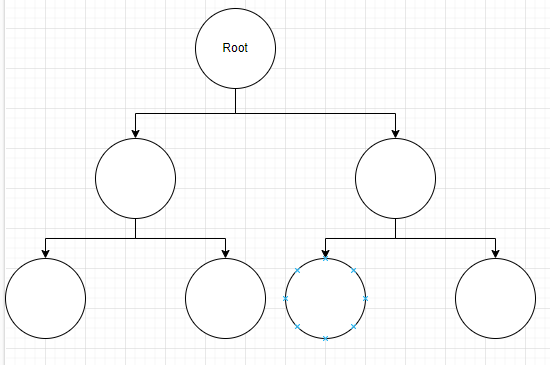
포화 이진 트리(Full Binary Tree) 는 위 사진과 같이 모든 레벨이 꽉 찬 이진 트리를 말합니다.
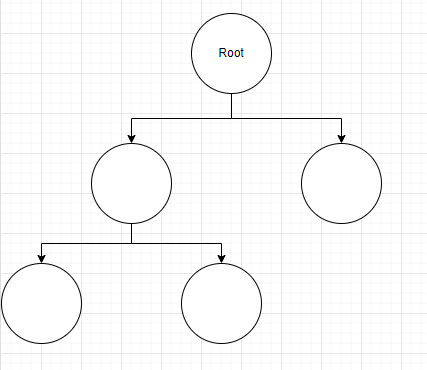
그와 달리 완전 이진 트리(Complete Binary Tree) 는 포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리를 뜻합니다.
이진 탐색 트리 구현하기
이번에는 이진 탐색 트리(Binary search Tree)를 구현해보겠습니다. 지금까지 계속 설명했던 이진 트리는 왜 구현하지 않느냐 하실 수 있지만 사실 아래에서 설명할 노드 클래스와 이진 트리에 대한 정의만 알고 있다면 그 구조를 만드는 것은 어렵지 않기에 생략했습니다. 코드는 유니티 C# 을 기반으로 작성하였습니다.
이진 탐색 트리는 이진 트리이지만 다음과 같은 특징을 추가로 가집니다.
- 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
쉽게 말해 다음과 같은 구조를 가지게 됩니다.
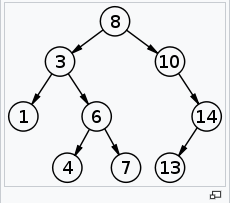
루트 노드를 기준으로 왼쪽 서브트리에는 루트 노드의 값보다 작은 값을 가진 노드들이 연결되어있습니다.
반면에 오른쪽 서브트리에는 루트 노드의 값보다 큰 값을 가진 노드들이 연결되어있습니다. 또한 모든 서브트리도 이와 같은 구조를 가지고있습니다.
이진 탐색 트리는 기본적으로 탐색을 위해 고안된 자료구조이므로 기본적으로 세 메서드를 구현합니다.
- 데이터 삽입
- 데이터 검색
- 데이터 삭제
먼저, 트리를 구성할 노드부터 정의할 수 있습니다.
public class Node
{
public int item;
public Node left = null;
public Node right = null;
public Node(int item)
{
this.item = item;
}
}
노드 클래스는 다음과 같이 구성되어 있습니다.
- int 형 데이터 변수 (반드시 int 형이 올 필요는 없습니다.)
- 왼쪽 노드를 가리킬 포인터 변수
- 오른쪽 노드를 가리킬 포인터 변수
이번에는 이진 탐색 트리(Binary Search Tree) 클래스를 정의합니다.
public class BST
{
// RootNode 변수
public Node root;
// Data 추가 메서드
public void AddItem(int item)
{
// 만약, 트리가 비어있다면 루트 노드를 생성
if (root == null)
{
root = new Node(item);
return;
}
// 현재 노드를 가리키는 변수를 root 노드로 초기화
Node curNode = root;
// 이전 노드를 가리키는 변수
Node prevNode = null;
// 현재 노드를 가리키는 변수가 어딘가를 가리고있다면 반복문 실행
// 반복문이 종료되면 curNode는 새 노드를 삽입할 자리를 찾게 됨
while (curNode != null)
{
// 이전 노드에 현재 노드의 주소 저장
prevNode = curNode;
// 현재 노드는 삽입할 노드의 데이터 값에 따라 현재노드의 왼쪽 혹은 오른쪽 노드를 가리킴
// 현재 노드의 값이 삽입할 값보다 크다면 현재 노드는 부모의 왼쪽 노드를 가리킴
// 현재 노드의 값이 삽입할 값보다 작다면 현재 노드는 부모의 오른쪽 노드를 가리킴
curNode = (curNode.item >= item) ? curNode.left : curNode.right;
}
// 이전 노드(부모 노드)의 값에 따라 왼쪽 혹은 오른쪽에 노드를 생성함
if (prevNode.item >= item)
prevNode.left = new Node(item);
else
prevNode.right = new Node(item);
}
}
이진 탐색 트리 내의 Add 메서드를 설명하기 위해 다음과 같은 상황이 주어져있다고 생각해봅시다.

이진 탐색 트리에서 7 이란 데이터를 가진 노드를 삽입하려 합니다. 이때, 가장 먼저 해야할 일은 당연 루트 노드와의 데이터 크기 비교일겁니다.
루트 노드의 데이터 크기는 8 입니다. 새 노드의 데이터는 7이기에 왼쪽 서브트리로 이동합니다.
이때 while 문 내부가 실행되며 curNode, preNode 포인터가 가리키는 노드가 바뀌게됩니다.
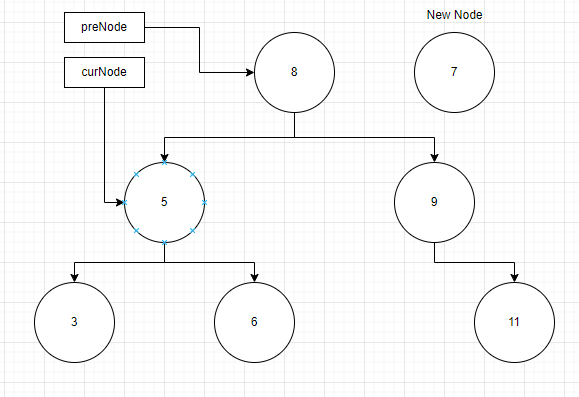
여기서 아직 curNode 가 다른 노드를 가리키고 있기 때문에 while 문을 계속 수행합니다. curNode 가 가리키는 노드의 데이터는 5이고 이는 새 노드의 데이터 크기보다 작으므로 curNode는 6을, preNode 는 5를 가리키게 됩니다.
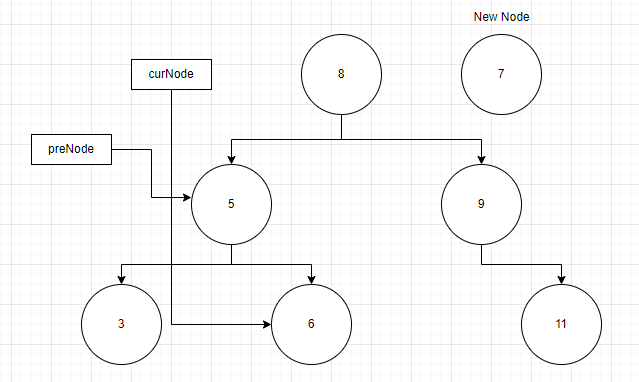
마지막으로 6이 7보다 작으므로 curNode는 6 노드의 right 노드를 가리키며 null이 됩니다. preNode는 curNode가 이전에 가리켰던 6을 가리키게 되면서 while 문을 빠져나갑니다.
while 문을 빠져나갔다면 조건문을 만나면서 새 노드를 추가하게 됩니다.
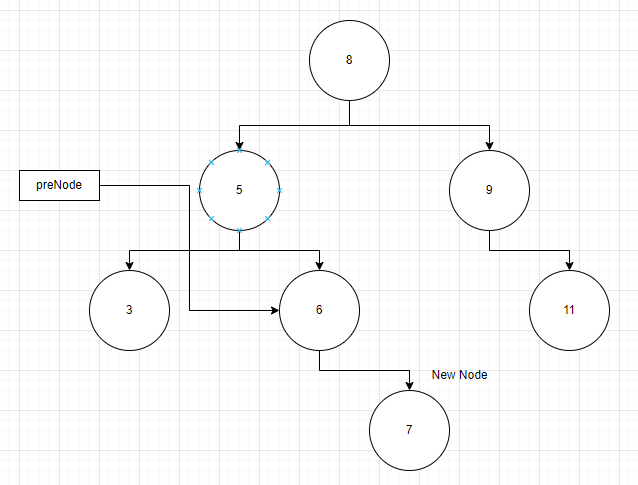
마무리
이번 포스팅에서는 트리에 대해 알아보고 이진 트리와 이진 탐색 트리에 대해 상세히 다루어보았습니다.
사실, 이진 탐색 트리는 데이터 검색을 보다 빠르게 하기 위해 고안된 자료구조이므로 검색 메서드가 구현이 되어야겠지만 글이 너무 길어지므로 코드만 따로 올려두도록 하겠습니다. 논리구조는 데이터 삽입과 크게 다르지 않습니다.
public class BST
{
public Node root;
// 탐색 메서드
public bool IsSearchItem(int item)
{
Node curNode = root;
int depth = 0;
while (curNode != null)
{
if (curNode.item == item)
{
Debug.Log(depth);
return true;
}
if (item < curNode.item)
curNode = curNode.left;
else
curNode = curNode.right;
depth++;
}
Debug.Log(depth);
return false;
}
}'자료구조' 카테고리의 다른 글
| 알고리즘 <삽입 정렬(Insertion Sort)> (0) | 2023.11.25 |
|---|---|
| 자료구조 <행동 트리(Behavior Tree) 기반의 AI 구현하기> (1) | 2023.11.24 |
| 자료구조 <이진 트리(Binary Tree) 데이터 순회> (0) | 2023.11.24 |


